-
[운영체제 만들기] Buddy Allcator프로젝트/운영체제 만들기 2023. 8. 7. 02:00
글의 참고
- https://en.wikipedia.org/wiki/Buddy_memory_allocation
https://gee.cs.oswego.edu/dl/html/malloc.html
https://koreascience.kr/article/CFKO200221138081397.pdf
글의 전제
- 내가 글을 쓰다가 궁금한 점은 파란색 볼드체로 표현했다. 나도 모르기 때문에 나중에 알아봐야 할 내용이라는 뜻이다.
- 밑줄로 작성된 글은 좀 더 긴 설명이 필요해서 친 것이다. 그러므로, 밑 줄 처친 글이 이해가 안간다면 링크를 따라서 관련 내용을 공부하자.
- `글의 참조`에서 빨간색 볼드체로 체크된 링크는 이 글을 작성하면 가장 많이 참조한 링크다.
- 대개 UEFI 에서 말하는 platform은 hardwares를 의미한다. 근데 구체적인 특정 하드웨어를 의미하기 보다는 Chipset 및 SoC를 의미하는 경우가 많다.
글의 내용
- 에러 사항
: 함수안에서 이중 포인터를 선언하고 비트맵에 대한 메모리를 참조하려고 했는데 , 계속 에러가 발생한다. ISR 13번이 발생한다. 이중 포인터를 전역으로 선언하면 에러가 안난다.
: 8바이트 출력이 없나? 이게 printf 포맷에서 `%d`는 부호있는 정수라고 해서 2,147,483,647까지만 출력되고 그 이후에 값들은 음수로 출력된다. 그런데, `%u`는 부호없는 정수라는데, 2,147,483,647 넘는 값을 작성하면 여전히 동일하게 음수가 출력된다. 일단 `%x`로 부호없는 4바이트는 어떻게든 버틴다고 해도 8바이트 출력은 2개로 나눠서 출력해야 하나??
- 메모리 레이아웃
- 64MB 부터는 메모리 관리 용도로 사용. 그 아래는 Boot 및 아키텍처 관련 정보들 저장.
- 10MB ~ 64MB : 64비트 커널이 사용.
: 이 커널 영역이 사용한다는 것이 감이 잘 안올 수 있다. 예를 들어, 메모리 관리 소프트웨어는 커널에서 거의 가장 빠른 시점에 초기화가 되야 하는데 그 메모리 관리 소프트웨어 에서도 메모리 관리를 위해 메타 정보들을 사용하게 된다. 예를 들어, yohdaOS는 물리적 메모리 관리를 위해 버디 할당자를 사용하는데, 실제 할당되는 데이터들을 관리하기 위한 메타 정보들을 만들어야 한다. 그런데 아직 메모리 관리를 위한 alloc(), free() 함수들이 만들어 지기 전이기 때문에 동적으로 메모리 영역을 할당받기가 어려워진다.
: 예를 들어, 동적 할당 영역이 정적으로 딱 정해지면 하드 코딩으로 블록 관리를 위한 메타 데이터들에 대한 개수를 하드 코딩할 수 있지만, 동적 할당 영역이 동적이라면 그 영역에 대한 관리를 위한 메타 데이터의 개수들 또한 동적이 된다. 이러면 사이즈를 딱 들어맞게 사용하고 싶은데 참 어려워진다.
: 그러면 메모리 관리 소프트웨어에서는 아직 초기화가 되기 전이니 동적 할당이 불가능하니 메모리 관리를 어떻게 해야 할까? 여기서는 OS 개발자가 임의의로 커널 영역의 메모리 범주(여기서는 10MB ~ 64MB)로 설정하고 이 영역안에 메모리를 이쁘게 잘 사용해야 한다.
이러면 동적 할당이 가능해지기 전까지 메모리 맵을 정확히 잘 짜서 데이터를 그에 맞게 관리할 수 밖에 없다.
- 1MB ~ 10MB " 32비트 커널이 사용.
- 버디 할당자 전제 사항
: 위키피디아가 정답은 아니지만, 그래도 누구도 무시할 수 없는 공신력을 가지고 있다고 생각한다. 그래서 위키피디아에서 정의한 버디 할당자 알고리즘에 대한 정의를 살펴보자.

출처 - https://en.wikipedia.org/wiki/Buddy_memory_allocation : 내가 정리를 해보면 구현에 필요한 부분은 다음과 같다.
1" 각 층의 블락 사이즈는 2의 제곱 사이즈를 갖는다.
2" 각 층의 블락이 2의 제곱 사이즈이기 때문에 상위 블락 사이즈는 대응하는 하위 블락 사이즈의 정확히 2배다.
3" 모든 버디 블락들은 메모리 주소는 2의 제곱 사이즈로 정렬되어 있다.
4" 제일 작은 블락 사이즈를 정해놓고 시작해야 한다. 요걸 기준으로 각 층에 필요한 블락 사이즈와 블락 개수를 설정할 것이다.
5" 가장 작은 블락의 층을 order-0-block이라고 정의하고 모든 상위 orders들은 가장 작은 사이즈의 2의 제곱 사이즈다.: 내가 생각하기에 가장 중요한 부분은 분홍색 부분이다. 이건 전체 메모리가 2의 제곱으로 나눠지지 않을 경우에 대한 케이스다. 예시에서는 2000K에서 상한선이 1024K라고 한다. 즉, 버디 할당자로 최대 할당은 1024K를 잡고 아래로 512K 2개, 256K 4개 .. 이런식으로 간다는 것이다. 나머지 976K는 더 작은 블록에 할당되어 한다고 하는데, 이 부분에 대한 구현은 나와있지 않다. 그래서 한 번 생각을 해보자. 976K를 어떻게 사용해야 할까? 버디 할당자 알고리즘은 각 블락의 사이즈가 2의 제곱을 전제로 한다. 그래서 2000K에서 1024K는 하나의 버디 할당자 알고리즘을 독단적으로 이루고 나머지 976K은 2의 제곱이 안되니 버디 할당자 알고리즘을 사용하기가 애매하다. 이걸 또 쪼깰까? 512K로 하면, 464K가 남는다. 즉, 2개의 버디 할당자 알고리즘을 사용한다? 얼마나 복잡할지는 모르겠지만, 사실 저렇게 할 수도 있다고 생각은 한다.
: 그렇면 2개의 버디 할당자 알고리즘을 했다고 치고 나머지 464K는 어찌할까? 좀 더 쪼갤 수 있으면 좋겠지만, 나는 이 부분을 나중에 슬랩 할당자에 할당하는 생각을 해본다. 슬랩은 캐시여서 사이즈가 좀 더 작아야 할 거 같긴 한데... 일단 초안은 남는 메모리가 많으면 2차 버디 할당자를 구현하고 남는 양이 적어지면 나머지 영역을 슬랩 할당자로 구현하려고 한다.
: 근데 만약 남는 사이즈가 없으면? 그래도 슬랩 할당자를 구현하긴 할 건데, 사실 문서를 안봐서 어떻게 메모리를 할당해야 할지 잘 모르겠다. ㄷㄹㄷㄹㄷㄹ8뎔89ㄷ결89ㄷ겨89ㄷ겨98혀89ㄷㄱㅎ
: 아래 코드의 차이가 뭘까? u32로 컨버팅되는 계산식은 정수 연산으로 처리된다. 그러나, 그 아래에 포인터끼리의 연산은 포인터의 데이터 타입에 따라 얼마나를 가감 및 차감 하는지가 달라진다. 즉, 포인터 타입이 `u32 *` 라면 +1을 하면 4바이트가 더해지고, -1을 하면 4바이트가 깍인다.
u32 **blocks; blocks[0] = 0x200000; blocks[1] = 0x210000; debug("buddy meta size#0x%x\n", (u32)blocks[1] - (u32)blocks[0]); debug("buddy meta size#0x%x\n", blocks[1] - blocks[0]);: 커널 영역에 할당되는 자료들은 절대 디스크 스왑이 되면 안되는 영역이다.
- 버디 할당자 초기화
: 내가 구현한 버디 할당자는 설계는 아래와 같다.
1" 각 층의 블락 개수 = 2의 거듭제곱
2" 각 층의 블락 사이즈 = 2의 거듭제곱: 각 층의 블락 개수가 2의 거듭제곱이면 분할 및 병합시에 코드가 상당히 간단해진다. 예를 들어. 144K를 힙으로 설정이 가능하다면 128K만 버디 할당 메모리로 사용하고 나머지 16K는 다른 메모리 방식으로 사용하는 것이다.
- 버디 할당자 상한 정하기
: 버디에서 적절한 상한을 정하지 않으면, 가장 큰 메모리를 요청하면 하나의 프로세스가 모든 메모리를 사용하게 된다. 그래서 YohdaOS는 최소 8개의 이상의 메모리 청크가 생기는 상한을 정한다. 깊이의 최대 상한은 11이고, 상한의 최소 청크 개수는 8이다. 이렇게 하지 않으면, 위에서 말한 것처럼 하나의 프로세스가 버디의 가장 큰 할당자를 요청하면 메모리를 독점하는 문제가 발생한다.
- 버디 할당자 최소 메모리 제한
: 버디 할당자를 사용할 경우, 비트맵에 대한 메타 데이터가 필요하다. 그러나, 사실 비트맵은 사이즈가 큰 자료구조는 절대 아니다. 그래도 버디 할당자에 매우 작은 양의 메모리를 할당할 경우, 메타 데이터 때문에 데이터 영역을 할당하지 못하는 경우가 발생할 수 있다. 그래서 YohdaOS는 버디 할당자에 할당 가능한 최소 데이터 사이즈는 256KB 이다. 만약, 255KB를 요청하면 버디 할당자를 사용하지 못한다. 이 뒤의 시나리오는 준비를 못했는데, Memory Pool에 할당을 하려고 한다.
- 버디 할당자 사이즈 구하기
: 메모리와 파일 시스템 관련해서는 데이터 영역과 메타 데이터 영역의 구분이 필요하다. 버디 할당자의 데이터 영역은 메타 데이터 영역을 뺀 나머지가 된다. 그런데 사실 명확하게 이 구분짓는 것이 쉽지가 않다.
버디 할당자 데이터 영역 = 전체 메모리 - 버디 할당자 메타 데이터 영역
: 메타 데이터라는 것은 데이터를 관리하기 위한 데이터를 의미한다. 그런데 이 메타 데이터 영역의 크기는 대부분 데이터 영역의 크기에 비례한다. 그리고 메타 데이터 영역의 크기는 데이터 영역의 크기를 알고 있어야 계산이 가능하다.
: 다른 하나는 메타 데이터 영역과 데이터 영역을 같이 구해나가는 것이다. 그러나 사실 이건 쉽지가 않다. 예를 들어, 메타 데이터에서 2개의 A와 B라는 자료 구조가 있다고 치자. 그런데, B라는 자료구조는 반드시 A라는 자료 구조를 만들고 나서야 가능한 구조라면, 상황이 힘들어진다. 왜냐면, 현재 메모리 관리는 직접 원하는 주소에 다이렉트로 매핑해서 진행하고 있고, 여기에
- 버디 할당자 구현 시 주의 사항
: 메타 데이터로 비트맵을 할당하고 나서 해야 하는 건 각 비트중에 `0`과 `1`의 의미 부여다. 즉, 0을 `할당 됨`으로 표시할지 `할당 가능`으로 표시할지 정해야 한다는 것이다. 이 값 설정에 대한 부분까지도 결국 자료구조다. 그렇면 구현에 보편적이면서 범용적인 커버가 되면서 직관적인 방법은 0을 `할당 가능`으로 표시하고 1을 `할당 됨`으로 표시하는 것이다. 즉, 0인 비트는 할당이 가능한 블락으로 설정하고, `은 이미 사용중인 블락으로 설정하는 것이다.
: 그 이유는 ㅈㄷㄹ389뎌823ㅕ89ㄱ 8설명필요.
: 그리고 나서 초기에 각 비트맵의 비트들을 어떻게 초기화해야 할지 정해야 한다. 그냥 전부 `할당 가능(0)` 이라고 표기하면 될까? 구현을 어떻게 하냐에 다르겠지만, 대개의 구현시 중요한 부분은 특정한 케이스에 대한 처리보다는 좀 더 범용적이면서 부분이 아닌 넓은 범위를 커버하는 구현을 한다는 것을 머릿속에 알고 가자.

: 위의 그림은 32KB 메모리에서 하한 블락 사이즈가 4KB인 버디 할당자 시스템이다. 4KB를 8비트 비트맵으로 관리한다고 전제해보자. 그렇면 가장 작은 블락 4KB는 1바이트(8비트)로 커버가 되고 꽉 채워서 관리가 된다. 그런데, 그 위층인 8KB 부터는 빈곳이 존재하게 된다. 즉, 1바이트로 처리는 가능하지만, 4비트가 남게된다. 그리고 그위에 16KB는 6비트가 남고, 32KB는 7개의 비트가 남게된다.
: 저 남는 비트들에 대한 초기 설정이 필요하다. 특징을 보면 8비트 비트맵을 사용할 때는 8개 미만에서는 여분의 비트가 남게된다. 만약 16비트 비트맵을 사용했다면 모든 층에서 여분의 비트가 남게될 것이다. 그렇면 우리는 사용 가능한 블락(비트)는 0으로 설정한다고 했으니, 사용되지 않는 비트를 어떻게 설정해야 할지 정해야 한다. 왜? 이 사용되면 비트들이 범용적이면서 일반적으로 구현된 알고리즘에 적용될 때, 값이 0이기 때문에 사용가능한 블락으로 오인될 소지가 있기 때문이다. 그렇기 때문에 값을 바꿔야 한다.
: 그럼 저 비트들은 몇으로 설정해야 될까? 비트는 0과 1밖에 없다. 0으로 설정하는 것은 안된다고 했으니, 1밖에 없는데 1로 해도되나? 우리는 비트가 1로 설정되면 현재 `사용 중인 블락`으로 설정하다고 했다. 그렇면 `사용되지 않는 블락`도 1로 설정해도 될까? 이제 이 문제를 고민해봐야 한다.
: 여기서 알고리즘의 내용을 들여다 봐야 한다. 알고리즘에서는 실제 32KB에 할당된 8비트 비트맵에서는 0번째 비트만 다룬다. 그리고 16KB 비트맵에서는 0~1번째 비트만 바라본다. 즉, 사용되지 않는 비트는 애초에 사용하지 않는다. 그럼 왜 `사용되지 않는 블락(비트)`를 신경써야 할까?
: 바로 아래의 바이트 오프셋을 구해야하는 부분 때문이다. 비트맵을 비교하는 부분을 보면, 하나의 비트맵(8비트 - 0xFF)이 사용중 이라는 것은 해당 비트맵의 비트들이 모두 1이라는 것을 의미하고, 이 말은 다음 비트맵을 검사해야 한다는 말이다( if(((*blk) & 0xFF) == 0xFF) continue; ).
int mm_find_free_byte(u8 dep) { u8 i; u8 *blk; if(dep < 0) { debug("Invalid Parameter#%d\n", dep); return -EINVAL; } for(i = 0 ; i < mm.bitmaps[dep].len ; i++) { blk = (mm.bitmaps[dep].block) + i; if(((*blk) & 0xFF) == 0xFF) continue; return i; } return -1; }: 위에서 만약 사용되지 않는 블락(비트)가 0으로 되어 있으면, 알고리즘의 문제가 발생할 수 있다. 예를 들어, 32KB 비트맵에서 실제 사용되는 비트는 0번째 비트만 사용한다. 알고리즘 설계 자체가 그러하다. 그렇면, 사용되지 않는 1 ~ 7번째 비트는 평생 0으로 되고, 이 말은 32KB만 사용 가능한 메모리에서 최소 32KB개는 계속 사용할 수 있다는 뜻으로 오해하게 된다.
: 그러므로, 초기화 시점에 여분의 비트가 존재하는 비트맵들은 사용되지 않는 여분의 비트들은 1로 설정하여 코드의 복잡성을 늘리지 않도록 설정하자.
: 만약 사용되지 않는 비트들의 1로 설정하지 않고, 0으로 두면서 저 위의 알고리즘에서 해당 케이스에 대해 예외처리를 하려면 어떻게 해야할까? 위의 예시는 8 비트맵을 사용하니 각층의 블락의 개수가 8개 미만인 층에 대한 예외처리를 해야 한다. 즉, 8KB, 16KB, 32KB에 대해 예외처리를 해야 한다. 물론 비트맵의 사이즈가 커지면, 4KB도 예외 처리를 해야한다. 물론 알고리즘을 바꿔야 하는 케이스 또한 많지만, 알고리즘에 if-else 케이스가 늘어나고 있다면 먼저 자료구조를 바꿔볼 것을 고려해보자.
: 블락 할당시에 저 부분을 별도로 처리한다? 좋지 않다. 왜냐면, 알고리즘 자체는 일반적이면서 범용적인것이 좋다. 즉, 예외 케이스를 두면서 많은 if-else문이 들어가는 것은 매우 좋지 않다. 그렇면 어떻게 하는게 좋을까? 자료구조를 이쁘게 짜면 된다. 알고리즘이 범용적이면서 일반적이게 되려면 자료구조를 짤 짜야 한다. 근데 이 자료구조에는 단순 구조체를 잘 짠다는 것도 있지만, 해당 구조체 및 변수에 어떤 값을 설정할 것인가에 대한 부분도 포함된다.
- 버디 할당자 구현 시 주의 사항
: 버디 할당자를 구현할 때, 실제 시간 복잡도는 O(n)이 대부분이다. 좀 더 자세하게 쓰면 O(n / 하나의 비트맵 크기) 인데, 시간 복잡도에서 상수는 의미가 없다. O(n)이 나오는 이유는 비트맵을 탐색할 때 대게 순차 탐색을 하기 때문이다. 그리고 순차 탐색을 통해 할당할 블락(비트)를 찾고 나서는 해당 블락(비트)에 대해 위, 아래로 이제 사용 중이라는 표시를 하게 되는데 이때는 이진 트리 형식의 탐색으로 표시를 한다. 이진 트리 탐색을 하니 O(log2n)으로 되지만, 시간 복잡도를 구할때는 더 많이 시간을 잡아먹는 시간 복잡도가 이기기 된다. 즉, n이 여러 개면 더 시간을 많이 잡아먹는 놈만 남는다. 그래서 결론적으로 O(n)이 된다.
: 이건 메모리 관리르 위한 메타 데이터의 사이즈를 줄이기 위해 비트맵을 사용하기 때문에 속도가 저렇게 밖에 나올 수 없다. 비트맵은 `0` 혹은 `1`에 대한 정보만 저장하기 때문에 트리형식으로 탐색하기에는 가지는 정보가 너무 부족하다. 만약, 속도에 신경쓰겠다면 트리 형식으로 바꿔 볼 수 있을 것이다.
- 버디 할당자 외부 단편화
: 아래 그림에서 버디 할당자에는 6K의 메모리가 남아있지만, 6K를 할당할 수 없다. 이렇게 실제 메모리의 물리적 공간은 남아있지만, 실제 할당이 불가능한 상황을 `외부 단편화`라고 하고, 버디에서도 외부 단편화는 발생한다.

: 버디에서 또 다른 외부 단편화의 예이다.
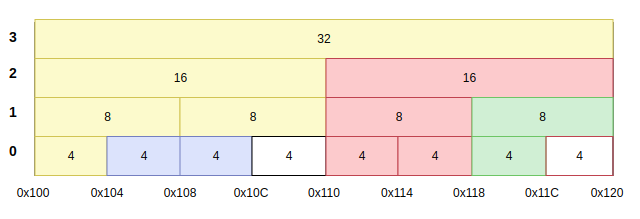
: 떨어져 있는 4KB 2개가 존재한다. 그러나 4KB를 초과하는 메모리를 요청할 경우 버디에서는 할당이 불가능하다.
- 버디 할당자 구현 시 주의 사항
: 버디 할당자를 구현할 때, 각 층의 블락들의 개수가 2의 제곱승 개수가 되지 않으면 어떻게 될까? 아래의 경우는 버디 할당자가 관리하는 메모리 영역이 43KB이고, 제일 작은 블락 사이즈가 4KB이며, 4-bit 비트맵을 이용한다고 가정한다. 일단 아래와 같이 메모모리 영역이 43KB이면 2의 거듭제곱 분할이 이상하게 된다.

: 4-bit 비트맵으로 각 블락들을 묶으면 다음과 같다.
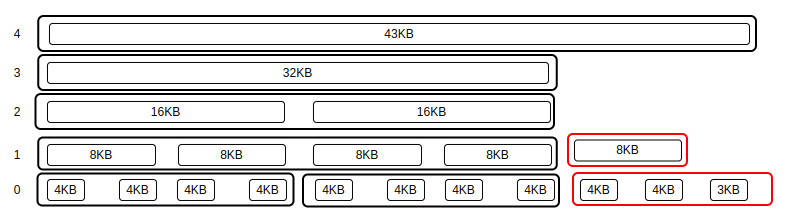
: 4 맨 오른쪽에 `4KB, 4KB, 3KB`는 애매하게 병합되지 못하게 남는 애들이 된다. 이 블락들에 대한 관리는 버디 할당자 알고리즘에 명시되어 있지 않고 OS 개발자가 상황에 맞게 구현을 해야한다. 나는 아래와 같이 구현했다.
"0 이들에게도 개수에 맞게 비트맵을 할당한다.
"1 이들에게도 분할 및 병합을 적용된다.: 위에서 `2` 번에 대해 좀 더 알아보자. 케이스를 좀 더 늘리자. 47KB와 52KB를 갖는다고 해보자.
: 각 깊이(order-n-block)에 할당되는 비트맵 개수는 다음과 같이 구할 수 있다.
order-n-block에 할당되는 4-bit 비트맵 개수 - ( 전체 사이즈 / n 번째 깊이 블락 사이즈 ) = A , A / 4 = B , A % 4 = C # B + C ? 1 : 0
order-n-block에 할당되는 8-bit 비트맵 개수 - ( 전체 사이즈 / n 번째 깊이 블락 사이즈 ) = A , A / 8 = B , A % 8 = C # B + (C ? 1 : 0): 계산은 아래와 같다.
" order-0-block에 할당되는 4-bit 비트맵 개수 - ( 47 / 4 ) = 11 , 11 / 4 = 2 , 11 % 4 = 3 # 3 + 1 = 4
" order-1-block에 할당되는 4-bit 비트맵 개수 - ( 47 / 8 ) = 5 , 5 / 4 = 1 , 5 % 4 = 1 # 1 + 1 = 2
" order-2-block에 할당되는 4-bit 비트맵 개수 - ( 47 / 16 ) = 2 , 2 / 4 = 0 , 2 % 4 = 2 # 0 + 1 = 1
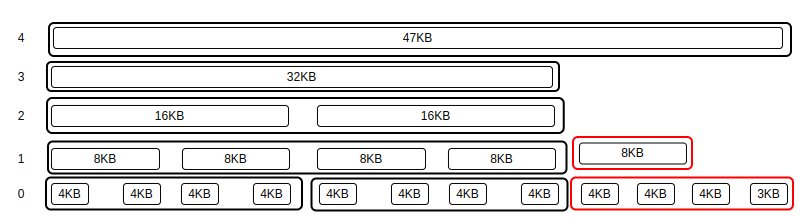
: 계산은 아래와 같다.
" order-0-block에 할당되는 4-bit 비트맵 개수 - ( 52 / 4 ) = 13 , 13 / 4 = 3 , 13 % 4 = 1 # 3 + 1 = 4
" order-1-block에 할당되는 4-bit 비트맵 개수 - ( 52 / 8 ) = 6 , 6 / 4 = 1 , 6 % 4 = 2 # 1 + 1 = 2
" order-2-block에 할당되는 4-bit 비트맵 개수 - ( 52 / 16 ) = 3 , 3 / 4 = 0 , 3 % 4 = 3 # 0 + 1 = 1
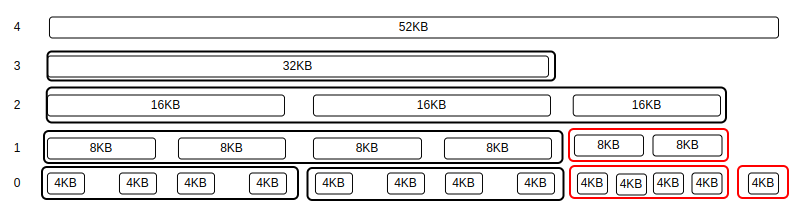
: 그런데 나는 좀 더 편리하고 심플한 방법으로 메모리를 관리하고 싶다. 버디 할당자는 일단 각 층의 개수가 2의 제곱 개수로 나와야 이상적이다.
- 버디 할당자 할당 구현
: 전체 메모리가 144K면 어떻게 버디 할당자를 만들어야 할까? 일단 버디 할당자는 하한(가장 작은) 블락 사이즈를 선택하는 것 부터 시작한다. 이걸 2K라고 전제하자. 그리고 나서 144K를 2K에 2의 거듭제곱을 계속 곱해가면서 144K를 나눈다. 몫이 0이 되는 지점 바로 직전이 가장 큰 블락의 상한이다. 즉, 128K가 상한 블락이 된다. 층은 7개로 이루어지는 것을 알 수 있다.
1" 144K / (2K * 2^0) = 64
2" 144K / (2K * 2^1) = 32
3" ...
7" 144K / (2K * 2^6) = 1
8" 144K / (2K * 2^7) = 0: 그렇면 나머지 16(144-128)K는 어떻게 해야 할까? 이 영역은 버디 할당자 알고리즘에서 특별히 언급되어 있지 않다. 그러므로, 다른 메모리 관리 방식을 사용하든 2차 버디 할당자로 사용하든 본인의 선택이 될 듯 싶다. 그럼 이제 여기서 15.4K를 할당받는다고 하면 일단 아래와 같이 블록들이 할당된다.
: 실제 붉은색 글자로 표시된 16K 블록만 할당받게 되지만, 실제 그 위의 데이터들은 사용하지 못하는 것을 볼 수 있다. 그리고 당연히 그 하위의 데이터들 또한 사용하지 못한다.

: 6.7K를 할당받아 보자. 8K를 할당받게 된다. 왼쪽부터 탐색하도록 설정해놨기 왼쪽부터 빈 공간이 있으면 메모리를 할당받게 된다.

: 1.2K를 할당받아 보자. 역시나 왼쪽의 할당이 가능한 공간부터 할당을 받는다. 위쪽 블락들이 사용하지 못하는 것에 집중하자.

: 43.7K를 할당받아 보자. 128K의 우측이 사용가능하므로, 해당 영역을 할당받게 된다. 하위의 모든 블락들은 사용할 수 없게 된다.

: 27.7K를 할당받아 보자. 역시나 빈 공간에 할당받게 된다.

: 그럼 이제 할당 시에 특징을 살펴보자.
1" 할당 시에는 할당되는 블락 기준으로 자신의 상위와 하위 블락들은 사용이 불가능하다.
2" 할당에는 순서를 정해야 한다. 위에서는 왼쪽부터 먼저 빈곳이 보이면 할당했지만, 구현 방법은 달라질 수 있다.: `"1`의 특징을 보면, 만약 자신의 바로 위의 블락이 이미 `사용 중` 상태라면 당연히 그 위위의 블락들 또한 `사용 중`인 블락이 된다는 것을 알 수 있다. 맨 처음 15.4K를 할당받을 때 붉은색 배경으로 체크되는 박스를 보면 알 수 있을 것이다. 15.4K를 할당받고, 6.7K를 할당받으려고 할 때, 상위 블락들을 사용할 수 없다는 표시를 해야하는데, 이미 앞에서 15.4K를 할당할 때 표시를 했으므로 상위 블락들에 대한 표식을 하지 않아도 된다.
: 하위 블락들에 대한 체크 부분은 간단하다. 할당받는 블락의 하위 블락들은 모두 `사용 중` 상태로 표시한다. 이 하위 블락들에 대해 탐색을 할 때, 각 깊이에 할당받은 블락 사이즈만큼으로 루프를 돌면서 하위블락들을 `사용 중` 상태로 바꾸면 된다.
: 만약 아래처럼 15.4K를 할당받으면 실제 16K 블락을 할당받게 될 것이다. 여기서 그 아래 2층부터 0층까지 루프를 돌아야 하는데 그 조건은 다음과 같다.
1" 2층은 2번
2" 1층은 4번
3" 0층은 8번: 규칙을 보면 한칸 아래로 내려갈 때 마다, 2의 거듭제곱으로 횟수가 늘어난다는 것을 알면된다.

: 6.7K를 받을 때도 마찬가지다. 6.7K를 요청하면 8K를 받게 되고, 아랙 그림은 알고리즘 구조상 가장 첫 번째로 발견되는 8K 블락이 할당된 모습이다. 그렇면 자식 탐색은 1층 2번, 0층 4번 루프를 돌면된다.

- 버디 할당자 해제 시 주의 사항
: 물리 메모리 할당자로 버디 시스템을 구현하면, 할당시에는 큰 고민없이 구현이 되지만 해제시에 조금 문제가 발생한다.
: 문제는 바로 `겹치는 물리 주소가 존재한다는 것`이다. 일단 함수를 좀 정의하자.
: buddy_malloc()과 buddy_free()가 존재한다고 하자. 각 함수는 아래와 같은 프로토타입을 갖는다고 하자.
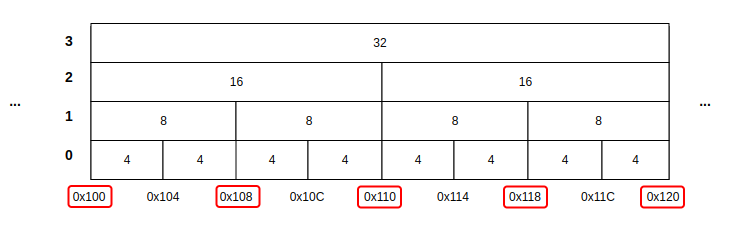
void *buddy_malloc(size_t size); void buddy_free(void* ptr);: 그리고 우리가 아래와 같이 노란색 배경으로 표시된 메모리는 할당된 것이라고 가정해보자.

: 사용자가 차례대로 `buddy_malloc(4KB); buddy_malloc(8KB); buddy_malloc(16KB);` 를 호출한 상황으로 가정하자. 그렇면 반환되는 주소는 다음과 같다.
buddy_malloc(4KB); - 0x100 buddy_malloc(8KB); - 0x108 buddy_malloc(16KB); - 0x110: 그런데 그 다음, `buddy_free(0x100)`를 호출했다고 하자. 그러면 당연히 맨 앞에 직관적이고 상식적으로 0x100을 해제하면 된다. 그런데 이게 코드상에서는 전혀 그렇지 않다. 코드상에서 0x100 번지에는 논리적으로 4개의 블락들이 존재할 수 있다. 그런데 `buddy_free(0x100)`는 주소만 전달하고 크기를 전달하지 않기 때문에 해당 주소를 기준으로 4KB를 해제해야 하는지, 8KB를 해제해야 하는지 알 수 없다.
: 이렇게 생각할 수도 있다.
비트맵을 저장할 때, 해당 정보(크기)를 같이 저장하면 되지 않나?
: 맞다. 근데 생각해보자. 버디 할당자 알고리즘은 메모리 관리에 대한 메타 데이터들의 사이즈를 최소화하기 위해서 `비트맵` 자료구조를 사용한다. 그래서 하한 블락 사이즈를 2KB로 잡고 4B(32비트)를 한 비트맵으로 잡으면, 각 비트마다 2KB를 관리할 수 있으니 하나의 비트맵으로 64KB를 관리할 수 있다. 그런데 여기에 각 블락마다 사이즈를 저장하면 메모리 관리를 위한 메타 데이터의 사이즈가 더 증가하게 된다. 심지어 하나의 최대 블락 사이즈가 만약 0x10000(65,536B)를 넘어가면 한 블럭당 4바이트의 메타 데이터가 추가된다. 근데 사실 아무리 생각해도 방법이 안보인다. 결국 메타 데이터를 더 추가해야 된다는 것인데, 그 사이즈를 최소화하고 싶다.
: 그런데 사실 정확한 표현은 `사이즈`가 아니라 `깊이`를 알아야 한다. 버디 할당자 알고리즘에서는 `깊이`와 `사이즈가` 서로 필요충분조건이기 때문에 사이즈를 알면 깊이를 알 수 있고, 깊이를 알면 사이즈를 알 수 있다. 그러나 사실 위의 문제의 근본적인 해결은 겹치는 주소에 대한 깊이만 알면 문제가 해결된다. 즉, 아래 그림처럼 32KB, 16KB, 8KB, 4KB의 주소가 모두 논리적으로 0x100에 할당되었지만, 깊이만 알면 이게 0번째 깊이의 주소인지, 1번째 깊의 주소인지, 2번째 깊이의 주소인지, 3번째 깊이의 주소인지 알 수 있다는 것이다.
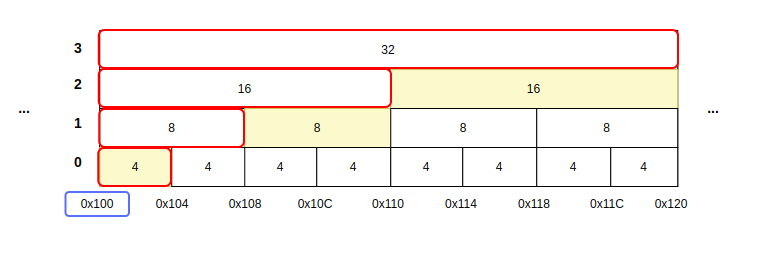
: 메타 데이터 사이즈를 최소화하기 위해서는 주소가 겹치는 부분을 곳을 유심히 보면, 주소가 겹치는 부분은 제일 작은 블락의 짝수 번째(0, 2, 4 ...)에서 등장한다. 요 블락들만 깊이를 같이 저장하면 되지 않을까? 일단 그래도 될 듯 하긴 한데 알고리즘의 복잡도의 문제가 너무 커지는 듯 하다. 그래서 나는 이 방법은 보류한다.
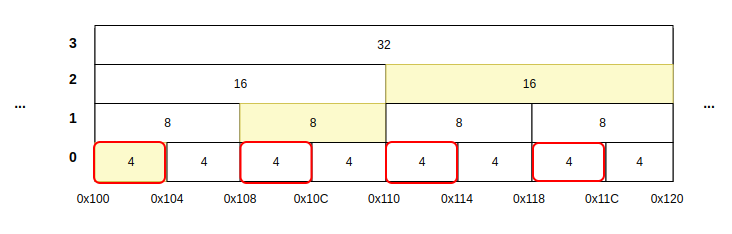
: 이제 더 이상의 고민없이 메타 데이터를 추가할거다. 그런데, 이 메타 데이터를 어느 영역에 저장할 것인가? 일반적으로 커널 영역에 대한 메타 데이터 저장 방법은 2가지가 있다.
1" 메타 데이터를 데이터 영역과 완전히 구분하고 별도의 영역에 몰아서 연속적으로 저장하기
2" 실제 사용되는 데이터 영역에 앞쪽에 헤더 형태로 저장하기: 비트맵 자료구조는 `한 영역에 몰아서 연속적으로 저장하기` 방식으로 메타 데이터를 저장했다. 이렇게 하면 뭐가 좋을까? 아래처럼 `메타 데이터`와 `데이터 영역`이 아예 구분되면서 메타 데이터를 연속적으로 저장하면 메타 데이터를 배열처럼 관리하기가 쉽다. 그리고 대게 많은 칩들에서 이렇게 자료구조를 연속적으로 제공해야 하는 경우가 거의 대다수다. 인텔만 해도 IDT 디스크립터, GDT 디스크립터등 대부분의 자료구조는 정렬이 된 상태로 제공해야 한다.
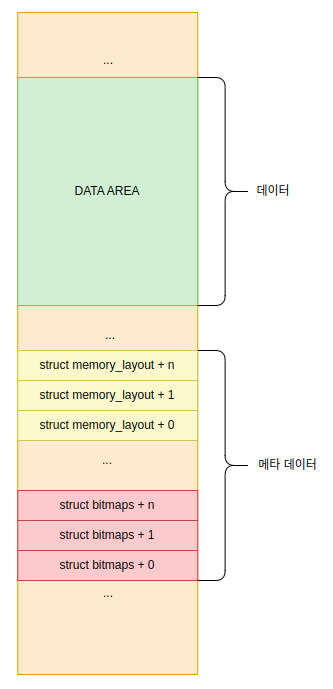
: 두 번째는 각 데이터앞에 헤더 형식으로 메타 데이터를 저장하는 구조다. 아래와 같이 각 데이터에 해당 데이터에 정보가 뒤 따라 붙게 된다. 대게 흔히 모든 데이터 통신은 되게 아래와 같은 구조를 띈다고 볼 수 있다.
: 나는 처음에는 2번 구조가 좋아보였다. 그리고 2번 구조는 2가지 유형을 나눌 수 있을 듯 싶다.
1" 데이터안에 헤더를 포함하는 형식
2" 데이터밖에(앞에) 헤더를 포함하는 형식: 그러나 사실 1번은 사용자를 속이는 것이다. 사용자가 2048B를 요청했는데, 헤더를 데이터안에 맨 앞에 붙이면 실제 2048B를 전부 사용할 수가 없게된다. 그러면 2번은 어떨까? 이건 사용자가 요청한 모든 데이터를 사용할 수 있게 해주지만, 복잡도 상당히 증가한다. 데이터를 하나 추가해보자.
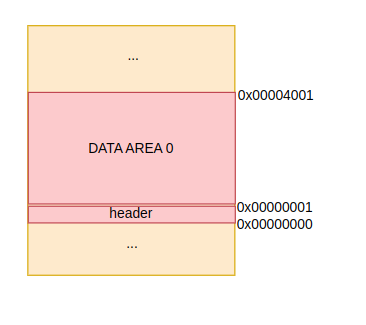
: 위 그림에서 보는 바와 같이 데이터앞에 헤더가 1바이트 붙는다고 치자.
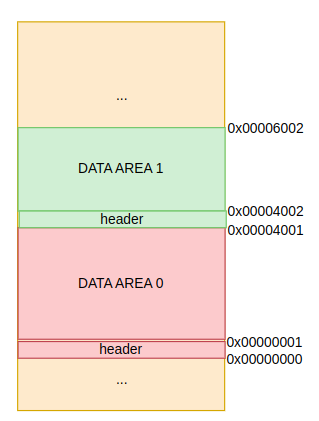
: 2번째 데이터는 그렇면 시작주소가 0x0000_4001이 된다. 그리고 데이터를 하나 더 추가해보자.
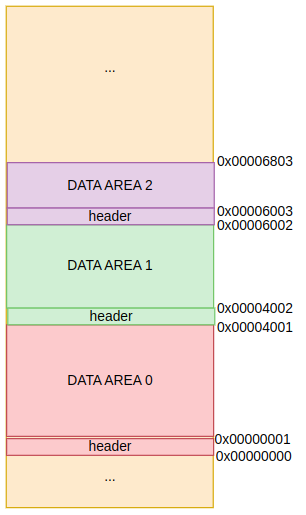
: 세 번째 데이터의 시작주소는 0x0000_6002가 된다. 그런데 여기서 64K가 추가된 것이다. 현재가 128K 버디 시스템이므로, 64K는 뒤쪽에 붙게된다. 앞에 데이터가 추가된 상태인데, 여기서 그렇면 시작 주소를 몇으로 해야할까?

: 그리고 32K가 하나 더 추가됬다. 32K의 시작주소는 몇으로 해야 할까? 여기서 할당받은 8K를 해제하고 새롭게 4K를 할당하면 시작주소를 몇으로 해야할까? 당연히 사람이라면 눈으로 딱 보고 8K가 해제되었던 곳(0x0000_4001)에 다시 할당하면 된다고 하면되지만, 컴퓨터가 이걸 계산하기에는 코드가 상당히 복잡해질 가능성이 높다.
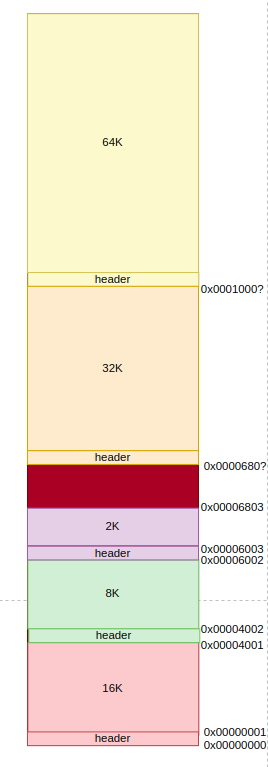
: 즉, 코드의 복잡성이 증가하는 것을 좋아하지 않기 때문에 나는 각 블락에 대한 깊이를 저장하는 메타 데이터 또한 데이터와 별도의 영역에 저장하는 방식을 택했다.
: 나는 근데 API 디자인을 아래처럼 하고 싶었다. malloc() 에서는 사이즈만 받고, free()에서는 malloc()에서 할당받은 주소만 전달해서 메모리를 해제하는 심플한 인터페이스를 유지하고 싶다.
void *malloc(size_t size); void free(void* ptr);: 그렇면 malloc() 시에 특정한 위치에 각 블락에 대한 깊이를 저장했다가, free()시에 전달받은 주소를 통해서 각 블락에 대한 깊이를 얻어내야 한다. 주소만 받아서 각 블락에 대한 깊이를 어떻게 알아내지? 주소와 헤더를 맵핑해야 한다.
func ( addr ) = order-`n`-block
: 각 힙의 시작 영역을 0x1000_0000에 가정하고, 각 블락에 대한 깊이를 0x0020_0000에서 부터 저장한다고 해보자. 각 깊이는 바이트라고 가정하자. 그렇면 일단 모든 블락에 대한 깊이를 알고 있어야 한다. 모든 블럭이란 몇 개일까? 즉, 버디 할당 시스템에서 모든 블락을 커버하는 할 수 있는 블락 개수가 몇개일까?
: 예를 들어, 힙 사이즈가 128K이고 가장 작은 블락 사이즈가 2K라고 해보자. 그럼 각 층의 블락 개수는 다음과 같다.
1" 144K / (2K * 2^0) = 64
2" 144K / (2K * 2^1) = 32
3" ...
7" 144K / (2K * 2^6) = 1
8" 144K / (2K * 2^7) = 0: 여기서 헷갈리면 안되는게 있다. 메모리는 하나다. 즉, 메모리는 128K로 하나다. 72K를 요청하면 128K가 할당되어 여분의 메모리가 존재하지 않아 할당이 불가능하다. 15.4K 요청이 들어오면 16K를 할당하게 되는데, 그 이후 메모리 할당 구조는 아래와 같이 된다.

: 16K를 할당하니, 128K는 당연히 사용하지 못하게 되고, 사용할 수 있는 가장 큰 블락이 64K이다. 그렇면 할당할 수 있는 최대로 블락이 되는 경우의 수가 어떤 경우일까? 바로 가장 작은 블락으로 모두 할당되는 경우다. 128K에서 2K로 모두 할당되면 64개의 블락을 할당할 수 있다. 우리는 이 64개의 블락에 대한 깊이를 별도로 저장하고 있으면 된다.
: 즉, `힙 사이즈 / 가장 작은 블락 사이즈 = 깊이에 대한 메타 데이터 개수`가 된다. 그렇면 위의 예에서 128K / 2K = 64 이므로, 64개의 메타 데이터가 필요하다고 판단할 수 있다. 그렇면 이제 매핑을 어떻게 시킬지 보자.
1" 0x1000_0000 -> 0x0020_0000
2" 0x1000_0800 -> 0x0020_0001
2" 0x1000_1000 -> 0x0020_0002
3" ...
64" 0x1001_F8000 -> 0x0020_0063: 위에서 실제 힙의 시작 영역을 0x1000_0000이라고 했다. 그렇면 위에서 16K를 할당해야 할경우, 버디에 할당된 블락이 현재 없으므로, 가장 먼저 찾게되는 주소영역을 반환하면 된다. 가장 먼저 찾게되는 주소가 해당 주소의 가장 앞쪽이 되므로, 해당 영역의 주소는 0x1000_0000가 된다. 그럼 이 주소와 깊이를 저장하는 데이터를 매핑해야 한다. 근데 이 하나의 테스트 케이스만으로 둘의 관계를 찾기가 어려우니, 다른 케이스도 한 번 보자.
: 6.7K를 요청했다고 해보자. 그렇면 이제는 앞에 16K가 이미 할당되어 있으므로, 주소 영역에 대한 계산이 필요하다. 8K는 2번째 깊이에 들어있고 앞에 16K가 할당되서 2개의 8K는 못쓴다고 보면 된다. 그렇면 3번째 8K부터 쓸수 있다. 그렇면 `힙의 베이스 + 3번째 8K의 주소`가 실제 반환하는 주소가 된다. 8K는 16진수로 0x2000된다. 그러므로, `0x1000_0000 + 0x4000`이 반환 주소가 된다. 이제 이 2개로 한 번 각 블락들의 깊이를 매핑시킬 수 있는지 보자.

: 16K의 힙 주소와 8K의 힙 주소는 다음과 같다.
1" ADDR(16K) = 0x1000_0000
2" ADDR(8K) = 0x1000_4000: 각 블락의 깊이 메타 데이터의 시작 주소는 0x0020_0000이다. 그리고 각 깊이는 1바이트라고 하자. 그렇면 각 블락의 깊이 메타 데이터 크기는 가장 작은 블락으로 힙을 모두 차지할 경우와 같으므로, 64가 된다. 0x1000_0000에서 128K(0x20000)를 차지하면 힙 영역의 사이즈는 0x1000_0000 ~ 0x1002_0000이 된다. 여기서 가장 작은 블락들이 각 깊이 메타 데이터와 매핑이 되야한다.
1" 0x1000_0000 -> 0x0020_0000
2" 0x1000_0800 -> 0x0020_0001
2" 0x1000_1000 -> 0x0020_0002
3" ...
64" 0x1001_F8000 -> 0x0020_0063: `buddy_free()` 함수에서 인자로 전달되는 값(반환 주소)에 포함하는 비트맵 깊이가 모두 다르기 다를 수 있기 때문에 비트맵 해제에 관한 메타 데이터 정보는 2번 방식을 택했다. 2번 방식을 택한 이유는 1번 방식으로 각 데이터 영역에 주소에 대한 깊이를 저장하려면, 최소 주소와 깊이와 함께 저장할 수 있는 자료구조가 필요할 것으로 보였다. 즉, 2개의 메타 데이터가 필요하다.
: 그런데 그냥 해당 주소앞에 해당 주소에 대한 깊이를 붙이면 주소를 별도로 저장하고 있어야할 의무가 없어진다. 왜냐면, 해당 주소 바로앞에 깊이가 존재하기 때문에 주소만 알면 깊이를 알 수 있게 된다.
: 대게 각 방식을 혼합해서 사용하고 전체 시스템 관리 차원에서 1번을 사용하고, 각 데이터별로 의미가 존재한다고 보는 경우에는 2번을 사용하는 것 같다.
: alloc()가 free() 함수를 보면, 함수의 프로토타입이 단순하다.
void *malloc(size_t size); void free(void* ptr);: malloc()은 사이즈를 받아서 해당 사이즈를 할당한 메모리 주소를 반환하고, free()는 해당 주소를 받아서 이전에 할당한 사이즈를 해제한다.
: 그런데 free() 함수에서 사이즈를 모르는데, 인자로 전달받은 주소에 대해 메모리를 해제할 수 있을까?
- 버디 할당자 쓰는 이유
: 버디 할당자는 `자동 합치기` 때문에 주로 쓰인다. 이렇게 하면 외부 단편화가 거의 발생할 수가 없다.
- 버디 할당자 쓰는 이유
: 버디 할당자의 order를 크게 늘리는 것은 좋은 방법이 아닌 듯 하다. 예를 들어, 133K를 버디 할당자로 배치할 경우 상한은 128K가 된다. 즉, 최대로 할당할 수 있는 메모리 크기가 128K라는 뜻이고 128K를 하나 할당할 경우 더 이상 다른 메모리는 할당이 불가능하다. 혹시나 저렇게 할당을 하더라도, 악의적으로 128K를 요청하면 다른 프로세스들은 메모리를 사용할 수 없어서 시스템이 마비가 될 것이다. 큰 메모리를 요청하는 프로세스는 반드시 특정 권한을 갖고 있어야 할 듯 싶다. 다시 본론으로 돌아와서, 위와 같은 문제로 버디에서는 상한을 올바르게 정하는게 무엇보다 중요하다고 생각된다.
: 상한을 정하는 부분은 할당하고 남는 나머지의 양과도 연관이 있다. 위처럼 133K를 할당하면, 운좋게 5K 정도가 남게된다. 그런데, 253K라면? 125K가 남게 되서, 이 남은 부분을 어떻게 사용해야 할지를 고민해야 한다. 그런데, order를 하단계만 낮춰보자. 즉, 64K를 상한으로 정한다면? 61K가 남게된다. 32K로 낮춰보자. 29K가 남게된다. 당연한 얘기였지만, 상한을 낮출 수록 나머지는 당연히 줄어든다. 문제는 버디에서 자연스러운 coalesce를 위해서는 크기뿐만 아니라 개수도 2의 거듭제곱으로 되어야 한다.
: 그러나 버디와 같이 automatically coalesce 기능이 있는 메모리 관리 방식도 거의 없기 때문에, 버디를 최대한 잘 활용해야 한다.
- 버디 할당자 최적화
: 버디 할당자 관련 내용을 알아보다 한국에서 2002년도에 나온 논문을 통해 버디의 성능 개선을 진행해보자. 이 논문은 2개의 리스트를 이용한다. QuickList와 BuddyList이다. Quick List는 작은 사이즈 블락들을 관리하고, BuddyList는 큰 블락 사이즈들을 관리한다. 그런데, 여기서 일단 문제를 제기할 수 있다. YohdaOS 또한 초기에 버디 할당자를 큰 메모리로 고정하고 Fast Memory pool을 이용해서 작은 메모리를 할당하려고 했으나, FreeBSD의 jemalloc
: 일단, 버디는 단연 비트맵을 최적화해야 한다. 각 블락 사이즈마다 비트맵이 존재한다. 즉, 2K 비트맵, 4K 비트맵, 8K 비트맵 등이 존재한다. 그런데 블락의 크기가 작아질 수록, 비트맵의 개수 또한 증가한다. 그래서 비트맵의 탐색에 시간이 오래 걸릴 수 있다.
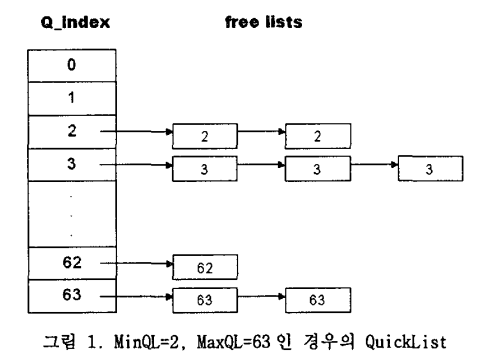
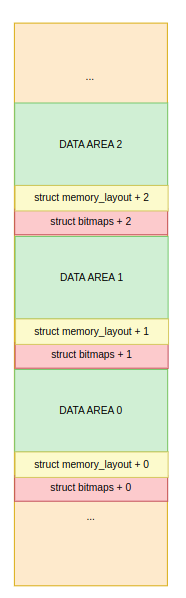
출처 - https://koreascience.kr/article/CFKO200221138081397.pdf : 그래서 이 논문에서는 아래와 같이 비트맵을 하나 더 선언하고 이 비트맵은 각 블락을 담당하는 비트맵에 FREE BLOCK이 존재하는지 없는지를 나타내는 역할을 한다. 아래에서 보면 0번 인덱스를 갖는 비트맵이 어느 사이즈 블락을 관리하는지는 모르겠지만, 해당 비트맵에서 3번째 블락을 사용할 수 있으므로, 세컨드 비트맵이 1이 된다. 이 1의 의미는 사용할 수 있는 블락이 있다는 의미이다. 그리고 Second_bitmap의 1번째 비트를 보면 0이다. 그 이유는 그에 대응하는 First_bitmap의 블락들이 모두 0 이기 때문이다.

출처 - https://koreascience.kr/article/CFKO200221138081397.pdf : 이 논문에서는 Second_bitmap은 First_bitmap의 8비트와 대응된다. 즉, First_bitmap의 8비트가 모두 0이면, Second_bitmap의 비트 한 개가 0이된다. 즉, First_bitmap의 8개의 비트가 Second_bitmap 1개 비트에 대응된다. 이렇게 하면 확실히 탐색 시간을 대폭줄일 수 있을것으로 판단된다.
'프로젝트 > 운영체제 만들기' 카테고리의 다른 글
[운영체제 만들기] ATA / IDE (0) 2023.08.07 [운영체제 만들기] Lazy Buddy Allocator (0) 2023.08.07 [메모리] Fixed-size blocks allocation (0) 2023.08.05 Real mode (0) 2023.08.05 Protected mode (0) 2023.08.05